Contents
Program Description
The equal area code is a Matlab function that attempts to divide polygons into smaller polygons of almost identical areas. This can be quite useful for statistical analysis of spatially heterogeneous data.
The code provided in this page covers two different techniques:
The first method has been developed by Scott 1990. (The reference was quite hard to find it. In fact I owe many thanks to Dylan Boyle who brought this up). The Scott method works quite well for relatively simple geometries. However for complex, especially highly non convex with islands, geometries there are several issues, which are highlighted below.
To alleviate the shortcomings of the Scott method I came up with the Metis method (at least that’s how I call it). In Metis method I use the metis code to do the hard work. The metis code is a software written primarily for partitioning graphs, partitioning finite element meshes, and producing fill reducing orderings for sparse matrices. However if we describe a polygon as a set of uniformly distributed connected nodes, we can use metis to partition that hypothetical mesh into smaller sets with equal number of nodes. This is a common problem in distributed computing and metis is known to perform very well.
How to use
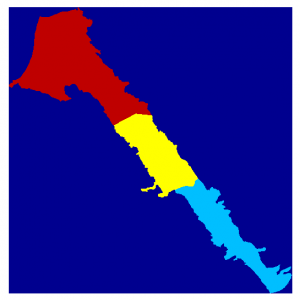
The workflow in both methods is very similar. First we have to represent the area as a Matlab matrix. If the area is described by a vector shapefile we can use a GIS software to rasterize it. The raster is essentially a matrix with numeric values on each cell. In this case the numeric values represent polygon ids. Both ArcGIS and QGIS software provide export to ascii files. To read the ascii GIS files we can use readArcGisASCIIfile matlab functions which is part of the mSim software, that can be downloaded from this website also. The following commands read the GIS ascii file, convert the nodata entries of the matrix to nan just for visualization purpose and plot the matrix:
|
1 2 3 4 5 |
[SVdata info] = readArcGisASCIIfile('../Data/sv_area_100.txt'); SVdata(SVdata==info.NODATA_value) = nan; image(flipud(SVdata)*20+20) axis equal axis off |
Scott Method
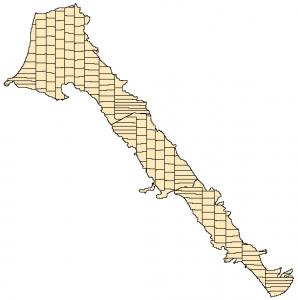
From a user perspective the Scott method involves just one line of code. The code below first converts the nans to a negative value to represent nodata values and calls the main function. The output of the Equal_Area function is another matlab matrix (essentially a raster) that has nan values everywhere except the areas that were selected for splitting (in this example the areas with ids 0 1 and 2). Finally we convert the nans to a nodata value that the GIS softwares understand and we write the result into an ascii gis file. The function WriteAscii4Raster is also part of the mSim software.
|
1 2 3 4 |
SVdata(isnan(SVdata)) = -9; SV_scott = Equal_Areas(SVdata, 1000, [0;1;2], -9, 'scott', []); SV_scott(isnan(SV_scott)) = info.NODATA_value; WriteAscii4Raster('SV_scott',SV_scott,info.xllcorner,info.yllcorner,info.cellsize,info.NODATA_value); |
The ascii file can be easily imported as raster in GIS and then can be converted to vector as shown below
Metis Method
The above method works quite well for relatively simple geometries. However for more complex shapes the method generates adjacent equal areas with very different shape. For example some areas are quite elongated while others are almost squares. In addition the method creates discontinuous equal areas.
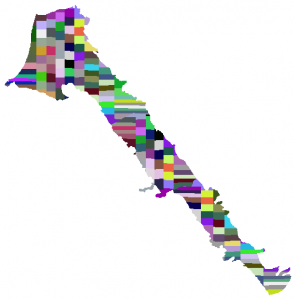
Using metis some of those issues can be reduced. The metis method does not require more work compared to Scott method yet one need to compile the code and produce the executable. The code snippet below assumes that we start with a clean Matlab workspace. Therefore the first step is to load the initial raster. Then we define a structure with the metis options. Metis code generates files. The name field of the opt structure specifies the prefix string to be used for those files. metis_path field is the path to the metis executable. The equal area function is almost identical with the difference that we specify the metis method and the option structure. Note that the metis method generates a lot of output in the workspace. Last we convert the nan values to numeric and write the data into ascii GIS format.
|
1 2 3 4 5 6 |
[SVdata info] = readArcGisASCIIfile('../Data/sv_area_100.txt'); opt.name='tempMetis'; opt.metis_path = '/home/giorgos/Downloads/metis-5.1.0/build/Linux-x86_64/programs/mpmetis'; SV_metis = Equal_Areas(SVdata, 1000, [0;1;2], -9999, 'metis', opt); SV_metis(isnan(SV_metis)) = info.NODATA_value; WriteAscii4Raster('SV_metis',SV_metis,info.xllcorner,info.yllcorner,info.cellsize,info.NODATA_value); |
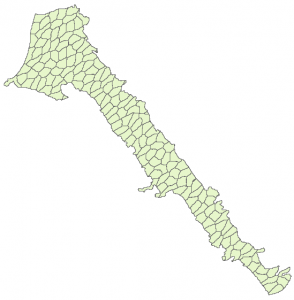
By comparing the results of the two method we can see that the metis method does not generates those elongated areas, however the areas are quite irregular.
Download
The code is just one Matlab function with few subfunctions contained within the same file. Simply copy paste the code from this link into a new file and save it as Equal_Areas.m
References
Examples that show how this method has been used can be found in the following references:
Boyle, D., King, A., Kourakos, G., Lockhart, K., Mayzelle, M., Fogg, G.E. & Harter, T. (2012) Groundwater Nitrate Occurrence. Technical Report 4 in: Addressing Nitrate in California’s Drinking Water with a Focus on Tulare Lake Basin and Salinas Valley Groundwater. Report for the State Water Resources Control Board Report to the Legislature. Center for Watershed Sciences, University of California, Davis. (Download)
Kourakos, G., and T., Harter (2013), A Validation Framework for Non-Point Source Simulation Models: Application to the Southern California Central Valley with Spatio-Temporally Heterogenous Source Rates. American Geophysical Union, Fall meeting 2013, San Francisco, California, USA.
Scott J. S., (1990), COMPUTERIZED STRATIFIED RANDOM SITE-SELECTION APPROACHES FOR DESIGN OF A GROUND-WATER-QUALITY SAMPLING NETWORK. U.S. GEOLOGICAL SURVEY, Water-Resources Investigations Report 90-4101.