Pumping Optimization

| main | Tutorials | Functions | website |

Contents

Introduction

In this tutorial we will show one of the advantages of mSim, its ability to be used seamlessly within an optimization framework. This example is based on the following assumptions

Assumptions

Problem description

The optimization problem is a typical dewatering problem: Find the minimum pumping amount that lowers the water table below a certain elevation.

Domain

Let's first create a simple example. Our example will be a rectangular domain of size 5000 m. The left and right boundaries are considered constant head with 30 and 40 m respectively, while the north and south boundary are impermeable. We will keep thing simple here. We will consider 6 wells around a site that we need to lower the water table.

The goal of optimization is to keep the water table around the center of the aquifer (2500,2500) at a radious 650 m below 30 m with the minimum possible pumping. There are two constraints regarding the well locations. The wells cannot be within the area we want to lower the water table and not close to the aquifer boundaries.

If you have followed any of the other tutorials the following snippet should make sense. (Here we do not explain in great detail the parts that the explanations can be found in other tutorials)

dom.Geometry = 'Polygon';
dom.X = [0 0 5000 5000 0 nan];
dom.Y = [0 5000 5000 0 0 nan];

domain = CSGobj_v2(2,1,10,10,1);
domain = domain.readshapefile(dom);

Let's create the mesh. Since the well locations are unknown we will generate a relatively fine but uniform mesh. If the well locations were constant then we would probably refine the mesh around them.

meshOptions = msim_mesh_options;
meshOptions.lc_gen = 50;
domain.writegeo('dewater_example', meshOptions);
gmsh_path='~/Downloads/gmsh-4.2.2-Linux64/bin/gmsh';
domain.runGmsh('dewater_example', gmsh_path, []);
[p, MSH]=read_2D_Gmsh('dewater_example', 0, 0);
Nel = size(MSH(3,1).elem(1,1).id, 1); % Number of 2D elements
Np = size(p, 1); % NUmber of nodes

Info    : Running '/home/giorgk/Downloads/gmsh-4.2.2-Linux64/bin/gmsh dewater_example.geo -2' [Gmsh 4.2.2, 1 node, max. 1 thread]
Info    : Started on Tue Mar 26 09:34:28 2019
Info    : Reading 'dewater_example.geo'...
Info    : Done reading 'dewater_example.geo'
Info    : Meshing 1D...
Info    : Meshing curve 1 (Line)
Info    : Meshing curve 2 (Line)
Info    : Meshing curve 3 (Line)
Info    : Meshing curve 4 (Line)
Info    : Done meshing 1D (0.000289 s)
Info    : Meshing 2D...
Info    : Meshing surface 1 (Plane, Delaunay)
Info    : Done meshing 2D (0.304119 s)
Info    : 13374 vertices 26750 elements
Info    : Writing 'dewater_example.msh'...
Info    : Done writing 'dewater_example.msh'
Info    : Stopped on Tue Mar 26 09:34:28 2019
Reading points...
Reading Elements...

Hydraulic properties, Fluxes, Boundary conditions etc.

Since the focus of this example is the optimization we will keep everything just simple. That means uniform hydaulic conductivity and recharge and no complex boundary conditions.

Hydraulic Conductivity

Assuming a uniform hydraulic conductivity and thickness we can define transmisivity on the nodes.

Tnd=100*ones(Np, 1); %m^2/day.

Fluxes

Groundwater recharge is the only flux considered in this example, besides the wells, with rate equal to 4 mm/day.

FLUX(1,1).id = [1:Nel]';
FLUX(1,1).val = 0.0004*ones(Nel,1);
FLUX(1,1).dim = 2; %is the dimension of the elements
FLUX(1,1).el_type = 'triangle'; %This is the type of element
FLUX(1,1).el_order = 'linear'; %This is the element order
FLUX(1,1).id_el = 1; %This is the index of the elements in the MSH.elem array

For the wells, their locations and rates will be determined via optimization. However we will add 6 wells in the model with random locations and rates that will be used as placeholders.

random_wells = [500 + 4000*rand(6,2) -(500 + 1500*rand(6,1))];

When the mesh of the domain was constructed the well locations where not taken into account. To assign the well fluxes in the mesh we will first identify in which elements the wells are laying and then assign the rate to the nodes of that element proportionaly with the distance from the nodes.

FLUX_point = [];

We need the element barycenters, and we initialize a weight vector

cc = Calc_Barycenters(p, MSH(3,1).elem(1,1).id);
weights = zeros(size(MSH(3).elem.id,2), 1);

Then for each well we find the distances from the element barycenter, and starting from the closest one we check if the well is in that element. This is actually always true so the loop breaks after jj = 1. The we compute the weights as the inverse distance from the element nodes.

for ii = 1:size(random_wells, 1)
    dst = sqrt((random_wells(ii,1) - cc(:,1)).^2 + (random_wells(ii,2) - cc(:,2)).^2);
    [c, d] = sort(dst);
    for jj = 1:length(d)
        in = inpolygon(random_wells(ii,1), random_wells(ii,2), p(MSH(3).elem.id(d(jj),:),1), p(MSH(3).elem.id(d(jj),:),2));
        if in
            node_distances = sqrt((random_wells(ii,1) - p(MSH(3).elem.id(d(jj),:),1)).^2 + (random_wells(ii,2) - p(MSH(3).elem.id(d(jj),:),2)).^2);
            if any(node_distances < 0.001)
                weights(:,1) = 0;
                weights(node_distances < 0.001,:) = 1;
            else
                weights = (1./node_distances)./sum(1./node_distances);
            end
            FLUX_point = [FLUX_point; MSH(3).elem.id(d(jj),:)', random_wells(ii,3)* weights];
            break
        end
    end
end

Boundary conditions

The nodes at the left side of the domain (x = 0), will be assigned a hydraulic head equal to 30 m.

id_left = find(p(:,1) < 0.1);
CH = [id_left 30*ones(length(id_left),1)];

The nodes at the right side (x = 5000) will be assigned a hydraulic head equal to 40 m

id_right = find(p(:,1) > 4999.9);
CH = [CH; id_right 40*ones(length(id_right),1)];

Assemble, solve, visualize

The following is the standard code to assemble the system matrices, solve the groundwater flow equation and visualize. (If you follow along the plot will look different than this one)

simopt.dim=2;
simopt.el_type='triangle';
simopt.el_order='linear';
[Kglo, H]= Assemble_LHS(p, MSH(3,1).elem(1,1).id, Tnd , CH, [], simopt);
F_rch= Assemble_RHS(length(H), p, MSH, FLUX);
F_wells = sparse(FLUX_point(:,1),1,FLUX_point(:,2),length(H),1);
Fall = F_rch + F_wells;
Hsol = solve_system(Kglo, H, Fall);
clf
trisurf(MSH(3,1).elem(1,1).id, p(:,1), p(:,2), Hsol(1:size(p,1)),'edgecolor','none', ...
    'FaceColor','interp','FaceLighting','phong');
camlight right
view(-40, 30);
drawnow

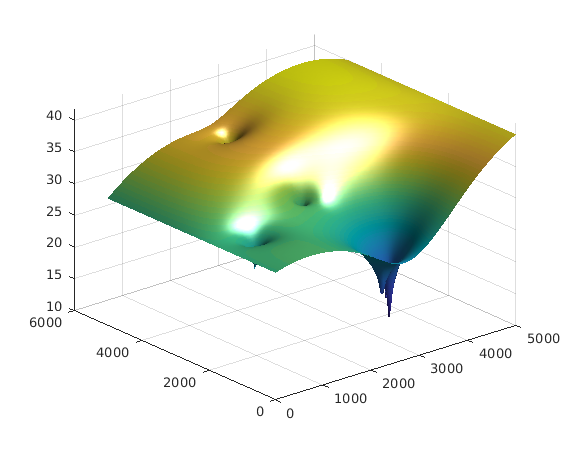
Getting ready for the optimization

In general, any optimization problem that involves the simulation of groundwater flow will actually solve a linear system of equations in the form KH = F where in our case K is the conductance matrix, F represent the fluxes and boundary conditions and H is the unknown vector. In this example we have made some assumptions so that the decision variables do not affect the matrix K. Therefore we can assemble the matrix K once and use it during the optimization. However we can further optimize the procedure.

Let's first delve into the system_solve function. The following snippet partitions the system to account for the boundary conditions.

First identifies the constant head nodes id_cnst and then partitions the matrices.

id_cnst=find(~isnan(H));
id_var=find(isnan(H));
KK=Kglo(id_var,id_var);
GG=Kglo(id_var,id_cnst);
DD=H(id_cnst);
B=Fall(id_var)-GG*DD;

After partitioning he actual system to solve is KK*H = B, which we can solve using the / matlab operator (lets repeat this many times to calculate an avarege solution time)

for ii = 1:200
    tic
    KK\B;
    t1(ii,1) = toc;
end

An alternative is to decompose first the matrix KK as:

[L,U,P,Q,R] = lu(KK);

and then solve (again repeat multiple times to get an average solve time)

for ii = 1:200
    tic;
    Q * (U \ (L \ (P * (R \ B))));
    t2(ii,1) = toc;
end
disp('K\B: sum, mean time in sec:')
disp([sum(t1) mean(t1)])
disp('Q * (U \ (L \ (P * (R \ B)))): sum, mean time in sec:')
disp([sum(t2) mean(t2)])

K\B: sum, mean time in sec:
    3.8356    0.0192

Q * (U \ (L \ (P * (R \ B)))): sum, mean time in sec:
    0.1971    0.0010

We can see than the latter is about 5% of the time when we use the first way of solving the system.

This maybe trivial for a single run but very important during an optimization that requires 1000s of runs.

Objective function

First we will create the objective function. The following code should be put in a separete file named as dewater_obj_fun.m (This file can be also found the repository)

The code penalizes the wells when they are inside to the dewatering area or far away from it. It also penalizes the solutions that violate the dewatering constraint, which is the groundwater elevation should be less than 30 m.

Important note: This objective function is not the best way to describe the constraints. In fact if you start the optimization from a non valid solution then the optimization will most likely fail, and this is because the objective function cannot guide the derivatives to suggest a path from infeasible to feasible space.

%{
function y = dewater_obj_fun(x, L, U, P, R, Q, GGDD, H, F, id_var, p, trimesh, cc, id_cnstr)
% x is a vector 6*3 of the decision variables.
% we reshape it so that they correspond to X Y Q
x = reshape(x, 6,3);
% distance from center
dst = sqrt((x(:,1) - 2500).^2 + (x(:,2) - 2500).^2);
% find if the wells violate the location contraints
id_in = dst < 650;
id_out = dst > 2000;

if any([id_in id_out])
    y = 100000*(sum(650-dst(id_in)) + sum(dst(id_out) - 2000));
else
    FLUX_point = [];
    weights = zeros(size(trimesh,2), 1);
    for ii = 1:size(x, 1)
        dst = sqrt((x(ii,1) - cc(:,1)).^2 + (x(ii,2) - cc(:,2)).^2);
        [~, d] = sort(dst);
        for jj = 1:length(d)
            in = inpolygon(x(ii,1), x(ii,2), p(trimesh(d(jj),:),1), p(trimesh(d(jj),:),2));
            if in
                node_distances = sqrt((x(ii,1) - p(trimesh(d(jj),:),1)).^2 + (x(ii,2) - p(trimesh(d(jj),:),2)).^2);
            if any(node_distances < 0.001)
                weights(:,1) = 0;
                weights(node_distances < 0.001,:) = 1;
            else
                weights = (1./node_distances)./sum(1./node_distances);
            end
            FLUX_point = [FLUX_point; trimesh(d(jj),:)', x(ii,3)* weights];
            break
            end
        end
    end
    Fall = F + sparse(FLUX_point(:,1),1,FLUX_point(:,2), length(H), 1);
    B = Fall(id_var)-GGDD;
    X = Q * (U \ (L \ (P * (R \ B))));
    H(id_var,1) = X;
    H_constraint = H(id_cnstr);
    id_violate =  H_constraint > 30;
    if any(id_violate)
        y = 100*sum((id_violate)) + abs(sum(x(:,3)));
    else
       y = abs(sum(x(:,3)));
    end
end
%}

Note that this objective function requires more inputs than just the vector of the decision variables. However the Matlab optimization algorithms require that the objective functions have just one input. According to matlab documentation we can create an anonymous function with one input with all other required inputs defined as parameters at creation time.

id_cnstr = find(sqrt((p(:,1)-2500).^2 + (p(:,2)-2500).^2) < 650);
f = @(x)dewater_obj_fun(x, L, U, P, R, Q, GG*DD, H, F_rch, id_var, p, MSH(3).elem.id, cc, id_cnstr);

Run optimization

Now we can run the optimization

We will define lower and upper limits for the decision variables and some optimization options. Finally we create a starting point that satisfy all the contraints and start the optimization.

lb = [500*ones(12,1); -5100*ones(6,1)];
ub = [4500*ones(12,1); 0*ones(6,1)];
fopt = optimoptions('fsolve','Display','final',... %
    'StepTolerance',1e-15,'MaxFunctionEvaluations',6000,...
    'DiffMinChange',10);%,'Algorithm','levenberg-marquardt'
xinit = [1000; 1000; 1000; 4000; 4000; 4000; ...
         1500; 2500; 3500;1500; 2500; 3500;
         -5000*ones(6,1)];
[x, fval, exitflag, output] = fmincon(f, xinit, [], [], [], [], lb, ub, [],fopt);

Warning: You have passed FSOLVE options to FMINCON. FMINCON will use the
common options and ignore the FSOLVE options that do not apply.
To avoid this warning, convert the FSOLVE options using OPTIMOPTIONS. 

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the selected value of the step size tolerance and constraints are 
satisfied to within the default value of the constraint tolerance.

Finally we can plot the results. As we did before we have to assemble the FLUX vector.

FLUX_point = [];
weights = zeros(size(MSH(3).elem.id,2), 1);
x = reshape(x, 6,3);
for ii = 1:size(x, 1)
    dst = sqrt((x(ii,1) - cc(:,1)).^2 + (x(ii,2) - cc(:,2)).^2);
    [~, d] = sort(dst);
    for jj = 1:length(d)
        in = inpolygon(x(ii,1), x(ii,2), p(MSH(3).elem.id(d(jj),:),1), p(MSH(3).elem.id(d(jj),:),2));
        if in
            node_distances = sqrt((x(ii,1) - p(MSH(3).elem.id(d(jj),:),1)).^2 + (x(ii,2) - p(MSH(3).elem.id(d(jj),:),2)).^2);
        if any(node_distances < 0.001)
            weights(:,1) = 0;
            weights(node_distances < 0.001,:) = 1;
        else
            weights = (1./node_distances)./sum(1./node_distances);
        end
        FLUX_point = [FLUX_point; MSH(3).elem.id(d(jj),:)', x(ii,3)* weights];
        break
        end
    end
end

and solve once more using the optimum solution

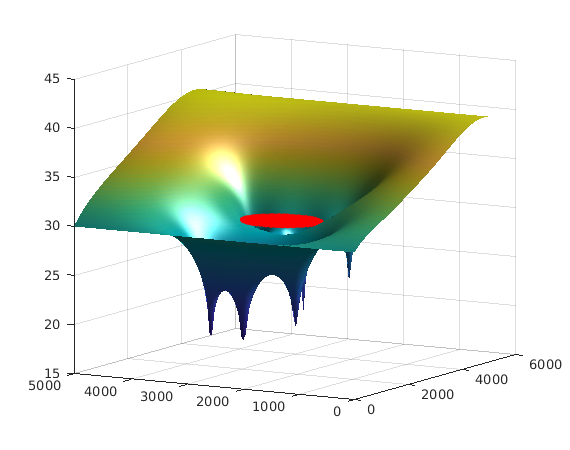
Hopt = solve_system(Kglo, H, F_rch + sparse(FLUX_point(:,1),1,FLUX_point(:,2),length(H),1));
clf
trisurf(MSH(3,1).elem(1,1).id, p(:,1), p(:,2), Hopt(1:size(p,1)),'edgecolor','none', ...
    'FaceColor','interp','FaceLighting','phong');
camlight right
view(-60, 10);
hold on
plot3(p(id_cnstr,1),p(id_cnstr,2),30*ones(length(id_cnstr),1),'.r')
drawnow;

We can see that indeed the water table around the area is lower than the constraint.

A tough question to answer: Is this indeed the optimum solution for this problem? Is this an appropriate algorithm to use?

References

We have used the above technique to the following papers:

| main | Tutorials | Functions | website |

Published with MATLAB® R2018a